Trigonometrie - vzorce
Pythagorova věta
V každém pravoúhlém trojúhelníku platí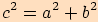 ,
kde
,
kde 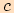 je délka přepony,
je délka přepony,
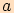 ,
, 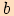 jsou délky jeho odvěsen.
jsou délky jeho odvěsen. Sinus úhlu 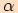
je poměr délky
protilehlé odvěsny k úhlu a délky přepony.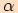
Kosinus úhlu 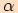
je poměr délky
přilehlé odvěsny k úhlu a délky přepony. 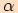
Tangens úhlu 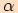
je poměr délky
protilehlé odvěsny k úhlu a délky přilehlé odvěsny.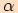
Kotangens úhlu 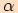
je poměr délky
přilehlé odvěsny k úhlu a délky protilehlé odvěsny.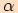
Sinová věta
Pro každý trojúhelník
 , jehož vnitřní úhly mají velikosti
, jehož vnitřní úhly mají velikosti
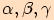 a strany délky
a strany délky 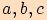 ,
platí
,
platí 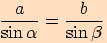 .
.Sinová věta Poznámka. Další vzorce vyplývají z principu cyklické záměny. Jsou to tyto:
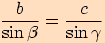
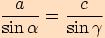 Sinovou větu můžeme také vyjádřit ve tvaru
Sinovou větu můžeme také vyjádřit ve tvaru 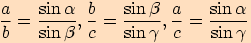 ,
,tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů k těmto stranám.
Kosinova věta
Pro každý trojúhelník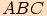 , jehož strany mají délky
, jehož strany mají délky
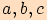 a jehož vnitřní úhel proti straně
a jehož vnitřní úhel proti straně
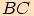 má velikost
má velikost 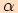 ,
platí
,
platí
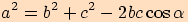 .
Poznámka. Jestliže ve vzorci pro kosinou větu přepíšeme
symboly stran a úhlů dle cyklické záměny, dostaneme vyjádření pro ostatní strany
.
Poznámka. Jestliže ve vzorci pro kosinou větu přepíšeme
symboly stran a úhlů dle cyklické záměny, dostaneme vyjádření pro ostatní strany 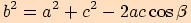 , kde úhel
, kde úhel 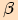 je úhel proti straně
je úhel proti straně 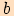 ,
,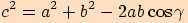 , kde úhel
, kde úhel 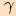 je úhel proti straně
je úhel proti straně 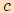 .
Poznámka. Pythagorova věta je vlastně speciálním případem
kosinové věty, jestliže je jeden úhel pravý, tzn.
.
Poznámka. Pythagorova věta je vlastně speciálním případem
kosinové věty, jestliže je jeden úhel pravý, tzn. 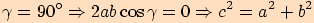 .
.Tangentova věta
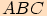 , jehož vnitřní úhly mají velikosti
, jehož vnitřní úhly mají velikosti
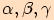 a strany délky
a strany délky 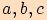 ,
platí
,
platí
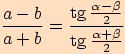 .
.
Poznámka. Další vyjádření tangentové věty dostaneme cyklickou záměnou. Jsou to vzorce:
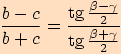
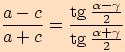
Vztah pro poloměr kružnice opsané trojúhelníku
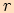 kružnice opsané trojúhelníku
kružnice opsané trojúhelníku 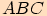 platí
platí  .
Obsah trojúhelníku pomocí dvou stran a úhlu jimi sevřeném
.
Obsah trojúhelníku pomocí dvou stran a úhlu jimi sevřenémPro obsah
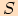 každého trojúhelníku
každého trojúhelníku
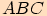 ,
jehož vnitřní úhly mají velikosti
,
jehož vnitřní úhly mají velikosti 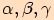 a strany mají délky
a strany mají délky
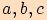 platí
platí 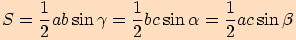 .
. Heronův vzorec
Pro obsah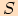 každého trojúhelníku
každého trojúhelníku 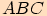 ,
jehož strany mají délky
,
jehož strany mají délky 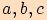 , platí
, platí
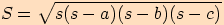 ,
kde
,
kde 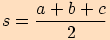 .
.
Poloměr kružnice opsané pomocí obsahu trojúhelníku a jeho stran
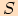 je obsah trojúhelníku
je obsah trojúhelníku 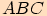 ,
jehož strany mají délky
,
jehož strany mají délky 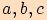 . Potom pro poloměr
. Potom pro poloměr
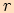 kružnice opsané tomuto trojúhelníku platí
kružnice opsané tomuto trojúhelníku platí
 .
.
Poloměr kružnice vepsané pomocí obsahu trojúhelníku a jeho stran
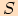 je obsah trojúhelníku
je obsah trojúhelníku 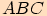 ,
jehož strany mají délky
,
jehož strany mají délky 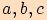 .
Potom pro poloměr
.
Potom pro poloměr 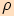 kružnice vepsané trojúhelníku
kružnice vepsané trojúhelníku 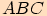 platí
platí
 ,
kde
,
kde 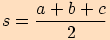 .
. Statistika
Statistika