Souhrn na pololetku - vlastnosti funkcí, lineární lomené - logaritmické funkce
Vlastnosti funkcí
Definiční obor - Df
Množina, ze které dosazujeme za y, určujeme ji z osy Y
Určování Df
Základní funkce (polynom) má Df = R
Pokud funkce není polynom, určíme podmínky, za kterých bude mít funkce smysl
1. zadání je zlomek
Jmenovatel se nesmí rovnat 02. zadání je odmocnina
Výraz v odmocnině nesmí být záporný3. zadání je logaritmus
Argument musí být větší než 0Obor hodnot – Hf
Množina, do které spadají funkční hodnoty bodu x, určujeme z osy X
Monotonie
- Rostoucí
- Klesající
- Konstantní
Prostá funkce
Funkce je prostá, jestliže jakákoli pomyslná rovnoběžka s osou y protne graf jen v 1 bodě
Omezenost
Jestliže je její funkční hodnota alespoň z jedné strany omezena
Určujeme na ose Y
Maximum, minimum
Hledáme na ose X
Nesmí to být interval
Sudá, lichá
Sudá – pokud je souměrná podle osy YLichá – souměrná podle počátku
Lineární lomená funkce
Předpis: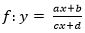
Df = R \ {– d / c}; (cx + d ≠ 0)

Dělení mnohočlenů
- 1. Vydělíme x-ka obou závorek,
- 2. výsledek vynásobíme 2. závorkou,
- 3. to odečteme od 1. závorky,
- 4. zbytek přičteme

Průsečíky
S X:
Př.: 
Za y dosadíme 0
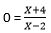
Vynásobíme jmenovatelem
0 = x + 4
Dopočítáme
x = - 4
S Y:
Za X dosadíme 0

Dopočítáme
y = - 2
Exponenciální funkce
Předpis: 
Df = R
a – kladné, kromě 1
V základu je průsečík s Y vždy 1
Graf - když je „a“ větší než jedna
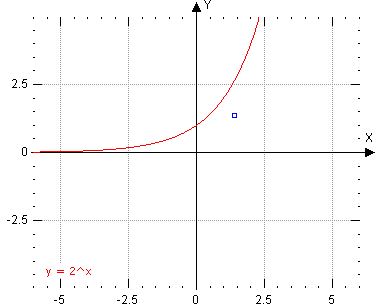
Graf - když je „a“ menší než jedna

Pravidla pro počítání s mocninami

Logaritmické funkce
Předpis: 
Df = (0 ; ∞)
a – kladné, kromě 1

S X:
Př.:
Za y dosadíme 0
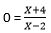
Vynásobíme jmenovatelem
0 = x + 4
Dopočítáme
x = - 4
S Y:
Za X dosadíme 0
Dopočítáme
y = - 2
Exponenciální funkce
Předpis:
Df = R
a – kladné, kromě 1
V základu je průsečík s Y vždy 1
Graf - když je „a“ větší než jedna

Graf - když je „a“ menší než jedna

Pravidla pro počítání s mocninami

Logaritmické funkce
Předpis:
Df = (0 ; ∞)
a – kladné, kromě 1

 Statistika
Statistika